이 글은 DATABASE SYSTEMS:The Complete Book(2nd Edition, Hector Garcia-Molina, Jeffrey D. Ullman, Jennifer Widom)의 Chapter3: Design Theory for Relational Databases를 요약/재구성한 글입니다.
스키마 설계 단계에서, 초안으로 나온 스키마는 개선의 여지가 많다. 제거해야 할 스키마의 중복(redundancy)이 대표적이다. 이런 관게형 데이터베이스의 이상(Anomalies)들을 쉽게 설명하기 위하여, 의존성(dependencies)이라는 개념은 좋은 수단이다.
우리는 함수의존성(FD, functional dependencies)의 아이디어부터 시작해서, 정규화(normalization)와 다치종속성(multivalued dependencies)이라는 이상 제거를 위한 개념들을 소개한다.
3.1 함수의존성(Functional Dependencies)
어떤 릴레이션 R의 함수의존성이라는 개념을 풀어 설명하자면, 이렇게 말할 수 있다.
“어떤 R의 두 튜플의 속성들 A1, A2, …, An이 모두 같으면(agree), 다른 속성들 B1, B2, …, Bn도 같아야한다.”
요약하자면 이렇다.

릴레이션 R의 두 튜플 t와 u에 대하여, 그림으로 표현하자면 아래와 같은 상황이다.

그리고 이렇게 표현한다.


실제 사례를 살펴보자. 오른쪽의 릴레이션은 chapter2에서 살펴본 Movie relation 보다 더 많은 속성을 포함하고 있고, 함수의존성도 존재한다. 우리는 title, year 값이 같은 두 튜플은 length, genre, studioName도 같을 것이라는걸 알 수 있다. 그래서 title과 year는 length, genre, studioName을 결정한다. 반면, starName은 length, year값이 같음에도 서로 다른 값을 가질 수 있다. 즉, 아래의 첫번째 FD(Functional Dependency)는 맞지만, 두번째는 틀렸다.
title year -> length genre studioName (맞다)
title year -\-> starName (아니다)
이 릴레이션에서 키는 {title, year, starName}이다. 어느 두 튜플들의 title, year, startName 값이 같다면, length, genre, studioName 또한 같을 것이다. 우리는 키를 두 가지 특징으로 다시 정의할 수 있다.
- 키의 속성들이 그 외의 나머지 모든 속성들을 함수적으로 결정(functionally determine)해야만 한다.
- 키의 어떤 부분집합도, 나머지 모든 속성들을 함수적으로 결정하지 못해야한다. {title, year} 만으로는 starName을 결정하지 못하는 것 처럼. 이것을 우리는 키의 미니멀리티(minimality)라고 한다.
키 집합을 포함하는 더 큰 속성들의 집합을 우리는 슈퍼키(superkey)라고 부른다. 슈퍼키는 앞선 첫번째 키의 조건은 성립하지만, 두번째 미니멀리티가 성립하지 않는다.
키는 한 릴레이션에 여러개일 수 있다. 이 키들을 후보키(candidate keys)라고 부르고, 그중에서 우리는 기본키(primary key)를 선택해야한다. 기본키는 FD 이론적으로는 다른 후보키들과 달리 취급될게 없지만, 현실의 데이터베이스 구현에서는 중요하다.
3.2 FD의 규칙들(Rules About Functional Dependencies)
FD와 관련된 몇가지 유용한 규칙과 용어들을 소개한다.
이행규칙(Transitive Rule)
“어느 릴레이션 R(A,B,C)에 대해서 FD A→B와 B→C가 성립한다면, R은 A→C도 만족한다.”
속성 하나가 아니라, 여러개에 대해서도 만족한다. 증명은 아래에서 소개할 개념인 클로져를 살펴 본 후에 할 수 있다.

분배/결합규칙(Splitting/Combining rule)
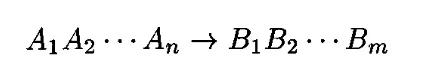

위의 FD가 성립하면 우변의 B들을 쪼개어, 아래의 FD들도 성립한다. 아래의 FD들이 성립하면 우변의 B들을 합쳐진, 위의 FD도 성립한다. B들에 대해서는 분배/결합이 가능하지만, A에 관해서는 불가능함에 주의한다.
동등성(Equivalence)
우리는 두 FD 들의 집합을 비교할 수 있다.
S = { A → B, B → C }
T = { A → C, A → B }
S와 T의 원소들은 달라 보이지만, S의 두 원소를 보면 A→C도 성립함을 알 수 있다. S를 만족하는 모든 인스턴스는, T도 만족할 것이다. 반대로 T를 만족하는 모든 인스턴스는, S도 만족할 것이다. 이것을 우리는 S와 T가 동등하다고 말한다.
R={ A→C }인 집합을 생각해보자. S로부터 R은 유도가능하다. 우리는 이것을 S가 R을 따른다(S follows from T)라고 한다. 반면, 이 경우는 R이 S를 따르지는 않는다. 두 집합이 서로를 따른다면, 그 두 집합은 동등하다.
자명성(Triviality)
아래의 식이 성립한다면, A1, A2, … An → B1, B2, …, Bn의 FD는 자명(trivial)하게 성립한다. 반사규칙(Reflexivity) 이라고도 한다.

예를 들어, title year → title 은 당연히 성립할 것이 예상가능하다. {title}은 {title, year}의 부분집합이다. 즉, 자명성을 쉽게 말하면, 오른편의 속성들이 왼편에도 똑같이 있으면, 자명히 성립한다는 뜻이다. 반대로 왼편과 오른편에 같은 속성이 없으면 자명하지 않다(non-trivial).
title year -> title (trivial FD)
title year -> length (non-trivial FD)
아래의 경우는 trivial 하지는 않지만, 성립하는 또 다른 명제이다.

어렵게 써있지만, title year -> title genre가 맞다면, 겹치는 title은 제외하고, title year -> genre도 맞을 거라는 것이다.
클로져(Closure)
어떤 속성 집합 {A1, A2, …, An}으로부터 어떤 FD 집합 S를 가지고, 함수적으로 결정할수 있는 모든 속성들의 집합을 {A1, …, An}의 클로져(Closure)라고 부른다.
S = { A->B, B->C }
X = { A }
X+ = { A, B, C } // X의 클로져
X는 속성 A만을 원소로 갖지만, FD 집합 S에 의해, B와 C의 값도 결정할 수 있다. A가 결정되는 것은 자명(trivial)하다. 따라서 X의 클로져는 {A, B, C}이며, X+로 표기한다.(+는 윗첨자에 있어야 하지만 편의상 이렇게 쓰겠다)
클로져 알고리즘
어느 속성집합 A과 FD집합 S로부터 A의 클로져를 구하는 알고리즘을 소개한다.
- FD 집합 S에서 분배할 수 있는 것들을 모두 분배한다.
- 새로운 집합 X를 정의한다. 초깃값은 A 그대로 한다.
- S에서 X의 원소들을 가지고, 새로운 원소를 결정할 수 있는 FD를 찾는다. 원소를 찾으면 X에 추가하고, 반복한다.
- 더 이상할게 없으면 이 때의 X가 주어진 A의 클로져다.
입력: 속성 집합 A, FD 집합 S
출력: A의 클로저 X = A+ X ← A
반복:
X에 새로운 속성이 추가되지 않을 때까지
S의 각 FD B → C에 대해
B ⊆ X이면, C를 X에 추가
이 알고리즘이 왜 성립하는지는 어떻게 증명할 수 있을까? 두가지를 증명하면 될것이다.
- 알고리즘의 출력값 X의 모든 원소들이, A와 S를 통해 결정될 수 있음. (정당성)
- 3의 과정에서 수학적 귀납법을 사용하면 증명가능하다. 초깃값인 A는 당연히 A로 부터 결정되고, 원소 하나를 추가해도 이건 A와 S로부터 결정할 수 있는 원소들임을 보인다.
- A와 S로 결정할 수 있는 모든 원소들이 X 안에 들어있음. (완전성)
- 귀류법으로 증명한다. Z는 두 속성 A와 S로부터 결정되는 속성이지만, X에는 빠져있다고 가정하면, 모순이 발생한다.
원소가 튜플 t와 s 두개 뿐인 인스턴스 I를 잡는다. t와 s는 A의 속성들에 대해서는 모두 같지만, 나머지에 대해서는 모두 다르다. 즉, A의 Z속성값과 S의 Z속성값은 다르다. 그런데, 우리는 Z가 A로부터 결정된다고 했기때문에, A의 속성들이 모두 같은 t와 s는 Z도 같아야한다. 모순이다.
- 귀류법으로 증명한다. Z는 두 속성 A와 S로부터 결정되는 속성이지만, X에는 빠져있다고 가정하면, 모순이 발생한다.
기저(Basis)
R(A,B,C)에 대해서 모두가 서로 결정적인 FD의 집합 S = { A→B, B→A, B→C, C→B, A→C, C→A }를 상상해보자. S의 원소들간의 중복을 확인할 수 있다. B = { A→B, B→C, C→A } 는 S와 동등하다. 이 때, B는 아래의 3가지 조건을 만족하는데, 이것을 최소기저(minimal basis)라고 한다.
- 모든 FD의 오른쪽 편에 속성이 하나뿐이다.
- FD 중에서 하나라도 사라지면, 더 이상 S와 동등하지 않다. 혹은 더 이상 S의 기저(basis)가 아니게 된다.
- FD 중에서 왼쪽 편의 속성 하나라도 사라지면, 더이상 S와 동등하지 않다.(기저가 아니다)
신기하게도, 어떤 릴레이션 R과 FD집합은 항상 하나의최소기저를 갖지는 않는다. 위의 S는 B 뿐아니라, 아래의 집합도 S의 최소기저이다.
C = { A→B, B→A, B→C, C→B }
암스트롱의 공리(Armstrong’s axioms)
아래의 세가지 공리이다. 1과 3은 이미 언급했다.
- 반사규칙(Reflexivity): 앞서 자명성에서 언급한 성질이다. X ⊇ Y 이면, X → Y
- 부가규칙(Augmentation): X → Y 이면, X Z →Y Z
- 이행규칙(Transivity): X →Y 이고 Y →Z 이면, X → Z
FD 사영하기(Projecting FD)
어떤 릴레이션 R과 그 릴레이션의 사영 R1을 생각하자. R에서 성립하는 FD들의 집합 S가 있을때, R1에서 성립하는 FD들의 집합 S1을 구할 수 있을까? 예시와 함께 알고리즘을 소개한다.
Input: R(A,B,C,D)와 그 사영 R1(A,C,D), 그리고 R에서 성립하는 S = { A→B, B→C, C→D }
Output: R1에서 성립하는 FD의 집합 S1
- 초기 S_1은 빈 집합이다.
- R의 속성들의 모든 부분집합들에 대하여, 클로져를 찾는다. 그리고, 어떤 속성이 추가되었는지를 보고 새로운 FD들을 만들어, S1에 추가한다. 단, R1에 있는 속성들만 추가하면 된다.
- {A}+ = {A,B,C,D} 이므로 A→C, A→D 를 R_1에 추가. {A}+가 이미 R_1의 모든 속성을 포함하므로, A는 더이상 생각하지 않아도 좋다. 예를 들어, {A,C}+도 {A,B,C,D} 일 것이고, 여기서 새로운 FD를 찾을 순 없을것이다. 만약 {A}+가 {A,B,C,D}가 아니였더라면, AC→D를 R_1에 추가했어야 할 것이다.
- {C}+ = {C,D} 이므로 C → D를 추가.
- {D}+ = {D} 이므로 새로운 비자명한(non-trivial) FD는 없음. 추가할 것 없음.
- {C, D} + = {C, D}이므로 추가할 것 없음
- 위 과정으로 S1을 구했지만 이것은 최소기저(minimal basis)가 아니다. 암스트롱의 공리로 중복된 기저들을 정리하면 A→D는 제거되고, {A→C, C→D}가 남는다.
3.3 관계형 데이터베이스 설계(Design of Relational Database Schemas)

위 릴레이션에는 3가지의 이상(anomalies)가 있다.
- 중복(Redundancy): year, length, genre가 중복으로 포함됨
- 수정이상(Update Anomalies): Star Wars의 length를 124에서 125로 수정하려 하니, 3번이나 수정해줘야한다.
- 삭제이상(Deletion Anomalies): Gone With the Wind의 Vivien Leigh 배우 정보를 삭제하려고 하니, Gone With the Wind 튜플 전체가 사라져 영화 자체의 정보도 남지 않게 된다.
이 문제들을 해결할 접근 방법 중 하나는 릴레이션을 분해(decompose)하는 것이다. 위 Movies1 relation을 Movies2와 3로 분해한 것은 아래와 같다. Movies2와 Movies3의 속성들의 합집합은 Movies1과 같아야한다.

이제 위 3가지 이상를 다시 살펴보자
- year, length, genre는 더 이상 중복되지 않는다.
- 이제 한번만 Star Wars의 length를 변경해도 충분하다.
- Vivien Leigh 정보를 삭제해도, 영화에 대한 정보는 남아있다.
혹자는 Movies3에 아직 title과 year의 중복이 남아있다고 할 수 있지만, 그 둘은 키이기 때문에 경우가 다르다. 또는, Star Wars의 year를 수정하고자 하면 여전히 문제가 남아있다고 할 수 있지만, 마찬가지로 그 둘은 키이다. 키들을 수정하거나 삭제하려고 하면, 이 릴레이션이 만족해야하는 FD 집합도 달라지게 된다.
Boyce-Codd Normal Form(BCNF)
이런 이상들이 존재하지 않는 형태의 릴레이션이 있다. 그 예로 BCNF를 소개한다. BCNF의 정의는 다음과 같다.
릴레이션 R이 BCNF ↔ 모든 R의 자명하지 않은 FD에 대해서, 왼편의 속성들이 R의 슈퍼키여야 한다.
앞서, Movies1 relation에서 키는 {title, year, starName} 이였는데, title year → length genre FD 역시 성립했다. 이 왼편의 속성들은 슈퍼키가 아니므로, Movies1은 BCNF가 아니다.
속성이 두 개 뿐인 릴레이션은 항상 BCNF다. 속성 A,B에 대해 A→B, B→A이 두 FD가 각각 성립할때/하지 않을때 2x2 가지 경우를 따져보면 모두 BCNF일수 밖에 없음을 확인할 수 있다.
어떤 릴레이션을 BCNF들로 분해하고 싶다면, 어떻게 해야 할까? 아래의 예를 통해 살펴보자
R(title, year, studioName, president, pressAddr)에 대하여,
title year -> studioName
studioName -> president
president -> presAddr이 성립함.
이 때 키는 {title, year}임을 알 수 있다.
1. BCNF의 조건이 성립하지 않는 FD 하나를 골라, 왼편 속성들의 클로져를 찾는다.
예)
- studioName -> president를 고르고
- studioName의 클로져는 {studio, president, pressAddr}
2. 방금 고른 FD의 왼편은 제외하고, 위 속성들을 기존 릴레이션에서 분리한다.
예)
- studioName만 제외하고, 분리한다.
- R1(title, year, studioName)
- R2(studioName, president, pressAddr)
3. 모든 릴레이션이 BCNF 일때까지 R_1과 R_2에서 반복한다.
예)
- R1은 이제 BCNF
- R2는 president->presAddr 때문에 아직 BCNF가 아님. 이 FD를 골라서 한 번 더 분해하면
R1(title, year, studioName) R2(studioName, president) R3(president, pressAddr)
3.4 분해(Decomposition)
분해(Decomposition)는 항상 좋은가? 아래의 세 가지 속성을 살펴보자.
- 이상 제거(Elimination of Anomalies)
- 정보 복구가능성(Recoverability of Information): 분해된 튜플들을 조인하면 기존 릴레이션의 정보를 복구할 수 있는가?
- 의존성 보존(Preservation of Dependencies): 분해된 릴레이션들을 다시 조인하면, 기존 원래의 FD 집합과 같아지는가?
결론부터 말하면, 이 3가지를 모두 만족하는 분해는 없다. 앞서 소개한 BCNF는 속성 1, 2 만을 만족한다.
정보 복구가능성
릴레이션 R(A,B,C)가 R1(A,B)와 R2(B,C)로 분해됐다고 하자. 이 때, R1과 R2를 조인했을 때, 원래의 릴레이션과 동일한 결과로 복구된다면, 정보 복구가 가능한 것이다. 기존 튜플들보다 많아서도 안되고, 적어서도 안된다.
의존성 보존
Bookings(title, theater, city)
{ theater → city, title city → theater }
위 릴레이션을 살펴보자. 영화관은 어느 한 도시에 위치해 있고, 보고싶은 영화와 볼 도시가 정해지면 영화관이 정해지니, 현실적으로도 위 FD는 충분히 말이 된다.
이 릴레이션의 키는 무엇인가? 키의 정의에 의하면 두가지가 가능하다. {title, city}, {theater, title}.
theater→city를 기준으로 Bookings를 Bookings1(theater,city), Bookings2(theater,title)로 분해한다. 그러면, 뭔가 이상하다는 것을 알 수 있다. 이 두 릴레이션을 다시 조인하면 {title, city}는 더 이상 키도 아니고, title city → theater FD는 성립하지 않게 된다.
3.5 Third Normal Form
위에서 BCNF에는 의존성 보존에 있어서 문제가 있다는 사실을 알았다. 제3정규화(Third Normal Form, 3NF)는 BCNF보다 한층 완화된 릴레이션의 형태이다. 제3정규화를 소개하기 전, 제1정규화(1NF)와 제2정규화(2NF)를 먼저 소개한다.
제1정규화는 릴레이션 안에 배열이나 집합 등 어토믹(atomic)하지 않는 값이 들어있지 않은 릴레이션을 말한다. 만약 어떤 튜플의 필드가 {a,b,c}라면 각각 a, b, c를 값으로 갖는 3개의 튜플로 분해하여 릴레이션을 1NF로 만들 수 있다.
제2정규화는 어느 속성이 키의 전체 속성이 아니라 속성 일부에만 의존하지 않는 릴레이션을 말한다. 다른 속성들은 {A,B} 키에 의존하는데, 어느 속성은 {A} 키에만 의존한다면 부분 의존(partially dependent)이 남아있어서, 2NF가 아니게 된다.
제3정규화는 BCNF의 정의와 비슷하다. 모든 R의 자명하지 않은 FD에 대해서, 왼편의 속성들이 R의 슈퍼키여야 하는것이 BCNF의 정의였다. 3NF는 여기에 오른편의 속성들이 키의 일부인 것을 허용한다. 다르게 말하면, FD의 왼편이 슈퍼키가 아니고, 오른편도 키와 상관 없으면 3NF가 아니다.
3NF로의 분해과정은 (1)이상제거, (2)정보복구가능성, (3)의존성보존 중 (2)와 (3)을 만족한다. 아래의 알고리즘이 바로 그것이다.
추가예정
...(3NF 분해과정)
...(MVN, 4NF)
'개인 공부' 카테고리의 다른 글
| [데이터베이스 개론] 4. 대수적/논리적 쿼리 언어(Algebraic and Logical Query Language) (0) | 2025.04.22 |
|---|---|
| [데이터베이스 개론] 3. 고급 데이터베이스 모델(High-Level Database Model) (0) | 2025.04.22 |
| [데이터베이스 개론] 1. 관계형 데이터 모델(Relational Data Model) (1) | 2025.04.21 |
| [이산구조] 명제(Proposition) (0) | 2025.03.02 |
| [전산기조직] 논리 디자인의 기초 - Combinational Logic 편 (0) | 2025.03.02 |
