이 글은 Discrete Mathematics and its Applications by Kenneth H. Rosen, 8th Edition의 1.1~1.3 절을 재구성한 내용입니다.
이 글은 LaTeX 수식이 포함되어 있습니다. $\sum$ <- 이 기호가 제대로 보이지 않으면 새로고침 해주세요.
명제(Proposition)
참/거짓을 판단할 수 있는 평서문(Declarative sentence)
"x+5=10"은 명제가 아니다. x의 값에 따라 참/거짓이 달라지므로, 문장만으로, 진위를 판단할 수 없기 때문이다. 나중에 다루지만, 이 문장은 predicate라고 할 수 있다.
명제를 부정(Negation)하면 새로운 명제를 만들 수 있다. 혹은, 두개 이상의 명제를 합쳐서 하나의 새로운 명제(compound proposition)를 만들 수 있다. 이 때 쓰이는 논리연산자(logical operator)를 connectives라고도 부른다.
명제 p의 부정(Negation)은 $\neg p$, $\overline{p}$, $\sim p$, !p, p', Np 로 표현한다.
명제 p와 q의 논리곱(Conjunction)은 $ p \mathbin{\text{and}} q$이다. $p \wedge q$로 표현한다. p와 q 가 모두 참일때, 참이다.
명제 p와 q의 논리합(Disjunction)은 $ p \mathbin{\text{or}} q$이다. $p \vee q$로 표현한다. p 또는 q 둘 중 하나가 참일때, 참이다.
명제 p와 q의 배타적 논리합(Exclusive or)은 $ p \bigoplus q $ 혹은 $ p \mathbin{\text{XOR}} q $로 표현한다. p와 q의 참/거짓여부가 다를때, 참이다.
조건문(Conditional Statements / Implication)
p와 q가 명제일때, 조건문(conditional statement / implication) $ p \to q $ 는 명제 "If p, then q" 를 의미한다. 이 때, p를 가설(hypothsis), 혹은 전제(premise), 혹은 선행(antecedent)이라고 하고, q를 결론(conclusion), 혹은 결과(consequence)이라고 한다.
이 때, $ p \to q $ 는 p는 참, q는 거짓일때만, 거짓이 된다. 즉, p가 거짓이라면 q의 진위여부는 $ p \to q $ 의 값에 영향을 주지 않음에 주의한다. 또, 아래의 표현은 모두, "If p, then q"와 같은 의미이다.
- q if p
- p only if q
- when p, q
- q when p
- a necessary condition for p is q
- a sufficient condition for q is p
- p implies q
- q whenever p
- q provided that p
- p is sufficient for q
$ p \to q \mathbin{\text{and}} q \to p$ 를 $ p \leftrightarrow q $로 표현하며, 이중조건문(biconditional statement / bi-implication) "p if and only if q" 를 의미한다.
$ p \leftrightarrow q $ 는 $ p \to q $와 $ q \to p $ 의 논리곱이므로, p와 q가 모두 참이거나 거짓일때만 참이다. 전제(premise)가 거짓이면, 결론에 상관없이 전체 명제가 참이 되기 떄문이다. 아래는 또 다시 다 같은 의미이다.
- p is necessary and sufficient for q
- if p then q, and conversely
- p iff q
- p exactly when q
$ \mathrel{\neg}, \mathrel{\wedge}, \mathrel{\vee}, \mathrel{\to}, \mathrel{\leftrightarrow} $는 지금 나열한 순서대로 연산순서가 정해진다. 예를 들어, $ p \vee q \wedge r $은 $ (p \vee q) \wedge r $ 보다는 $ p \vee (q \wedge r) $ 로 연산되는 것이 일반적이다.
명제적 동등성(Propositional Equivalence)
Tautology
어떤 Compound Proposition을 구성하는 p, q등 변수들의 값에 관계없이, 항상 참이 되는 명제
모순(Contradiction)
어떤 Compound Proposition을 구성하는 p, q등 변수들의 값에 관계없이, 항상 거짓인 명제
아래 표는 가장 간단하게 만든 tautology와 contradiction의 예시이다.
| $ p $ | $ \neg p $ | $ p \vee \neg p $ (Tautology) |
$ p \wedge \neg p $ (Contradiction) |
| T | F | T | F |
| F | T | T | F |
$ p \leftrightarrow q $ 가 tautology이면, p와 q는 동치(logically equivalent)라고 하고, $ p \equiv q $ 라고 표기한다.
역(Converse), 이(Inverse), 대우(Contrapositive / Transposition)
$ p \to q $ 일때,
역: $ q \to p $
이: $ \neg p \to \neg q$
대우: $ \neg q \to \neg p$
어떤 명제 $ p \to q $와 대우 $ \neg q \to \neg p$ 는 항상 동치이다.
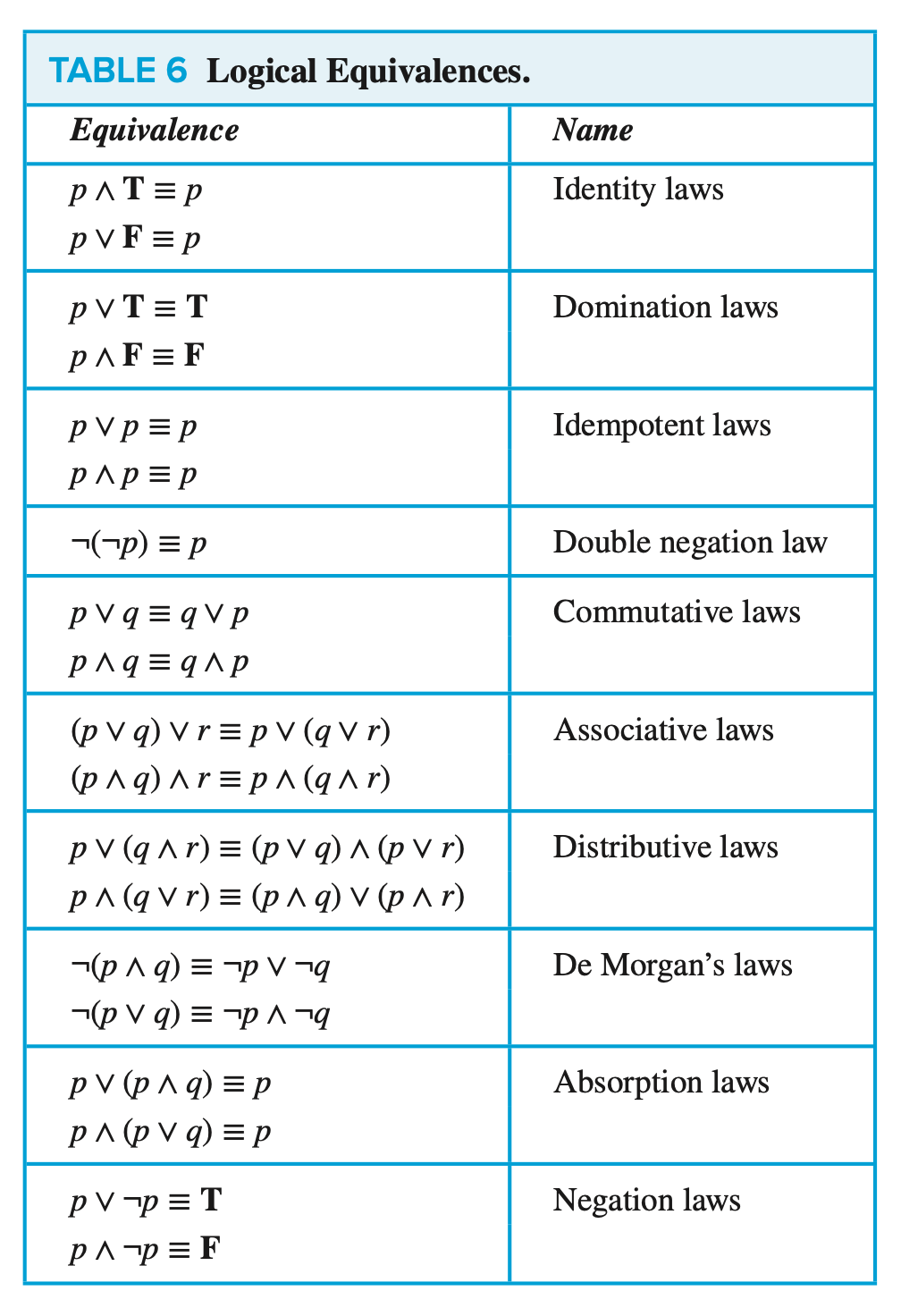
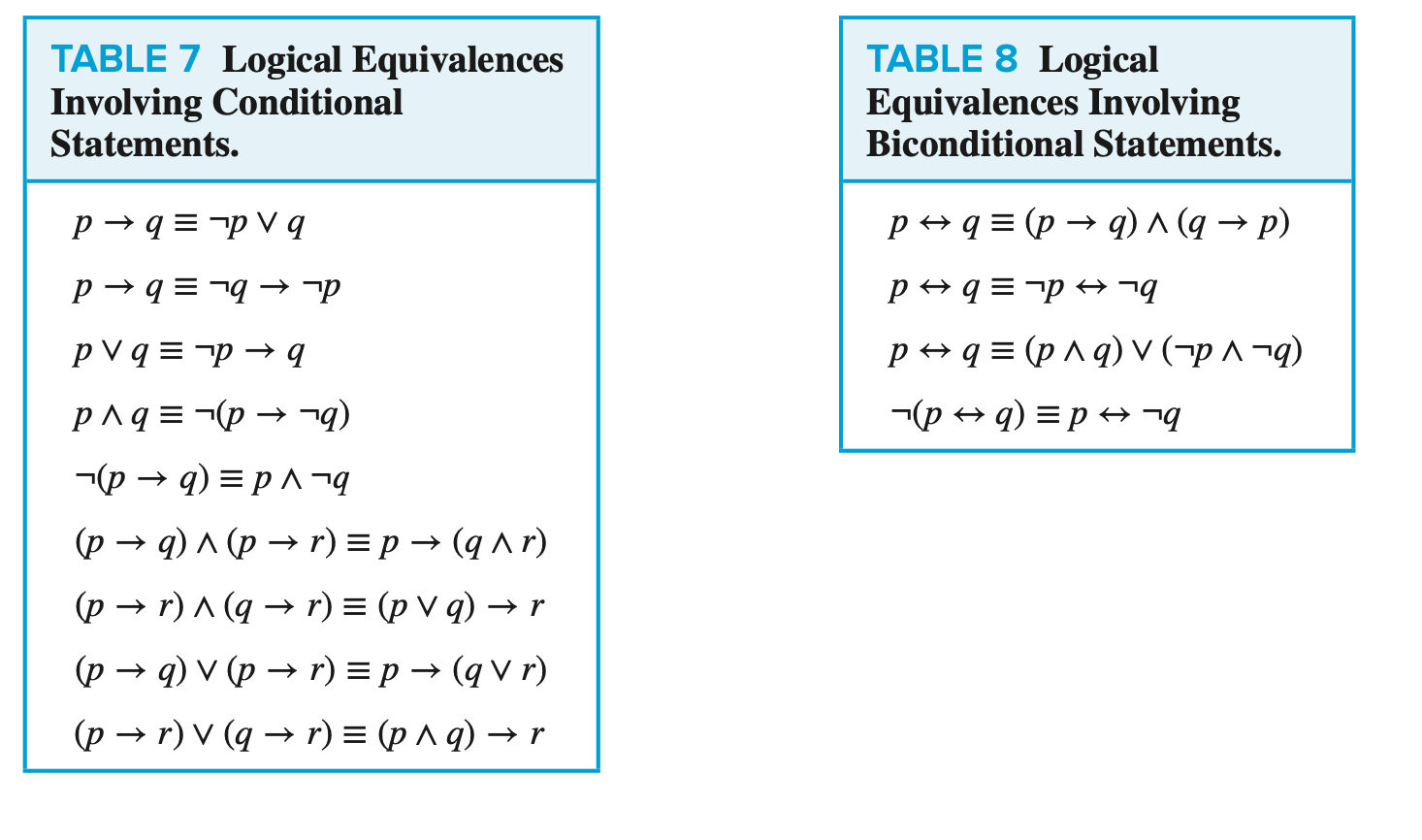
아래 표는 기본적인 동치들이다.
만족가능(Satisfiable), 불능(Unsatisfiable)
명제를 참으로 만드는 변수들의 조합이 존재하면 만족가능(Satisfiable), 존재하지 않으면 불능(Unsatisfiable)이다.
'개인 공부' 카테고리의 다른 글
| [전산기조직] 논리 디자인의 기초 - Combinational Logic 편 (0) | 2025.03.02 |
|---|---|
| [정보보호개론] 보안의 속성(CIA triad, AAA triad) (0) | 2025.02.28 |
이 글은 Discrete Mathematics and its Applications by Kenneth H. Rosen, 8th Edition의 1.1~1.3 절을 재구성한 내용입니다.
이 글은 LaTeX 수식이 포함되어 있습니다. $\sum$ <- 이 기호가 제대로 보이지 않으면 새로고침 해주세요.
명제(Proposition)
참/거짓을 판단할 수 있는 평서문(Declarative sentence)
"x+5=10"은 명제가 아니다. x의 값에 따라 참/거짓이 달라지므로, 문장만으로, 진위를 판단할 수 없기 때문이다. 나중에 다루지만, 이 문장은 predicate라고 할 수 있다.
명제를 부정(Negation)하면 새로운 명제를 만들 수 있다. 혹은, 두개 이상의 명제를 합쳐서 하나의 새로운 명제(compound proposition)를 만들 수 있다. 이 때 쓰이는 논리연산자(logical operator)를 connectives라고도 부른다.
명제 p의 부정(Negation)은 $\neg p$, $\overline{p}$, $\sim p$, !p, p', Np 로 표현한다.
명제 p와 q의 논리곱(Conjunction)은 $ p \mathbin{\text{and}} q$이다. $p \wedge q$로 표현한다. p와 q 가 모두 참일때, 참이다.
명제 p와 q의 논리합(Disjunction)은 $ p \mathbin{\text{or}} q$이다. $p \vee q$로 표현한다. p 또는 q 둘 중 하나가 참일때, 참이다.
명제 p와 q의 배타적 논리합(Exclusive or)은 $ p \bigoplus q $ 혹은 $ p \mathbin{\text{XOR}} q $로 표현한다. p와 q의 참/거짓여부가 다를때, 참이다.
조건문(Conditional Statements / Implication)
p와 q가 명제일때, 조건문(conditional statement / implication) $ p \to q $ 는 명제 "If p, then q" 를 의미한다. 이 때, p를 가설(hypothsis), 혹은 전제(premise), 혹은 선행(antecedent)이라고 하고, q를 결론(conclusion), 혹은 결과(consequence)이라고 한다.
이 때, $ p \to q $ 는 p는 참, q는 거짓일때만, 거짓이 된다. 즉, p가 거짓이라면 q의 진위여부는 $ p \to q $ 의 값에 영향을 주지 않음에 주의한다. 또, 아래의 표현은 모두, "If p, then q"와 같은 의미이다.
- q if p
- p only if q
- when p, q
- q when p
- a necessary condition for p is q
- a sufficient condition for q is p
- p implies q
- q whenever p
- q provided that p
- p is sufficient for q
$ p \to q \mathbin{\text{and}} q \to p$ 를 $ p \leftrightarrow q $로 표현하며, 이중조건문(biconditional statement / bi-implication) "p if and only if q" 를 의미한다.
$ p \leftrightarrow q $ 는 $ p \to q $와 $ q \to p $ 의 논리곱이므로, p와 q가 모두 참이거나 거짓일때만 참이다. 전제(premise)가 거짓이면, 결론에 상관없이 전체 명제가 참이 되기 떄문이다. 아래는 또 다시 다 같은 의미이다.
- p is necessary and sufficient for q
- if p then q, and conversely
- p iff q
- p exactly when q
$ \mathrel{\neg}, \mathrel{\wedge}, \mathrel{\vee}, \mathrel{\to}, \mathrel{\leftrightarrow} $는 지금 나열한 순서대로 연산순서가 정해진다. 예를 들어, $ p \vee q \wedge r $은 $ (p \vee q) \wedge r $ 보다는 $ p \vee (q \wedge r) $ 로 연산되는 것이 일반적이다.
명제적 동등성(Propositional Equivalence)
Tautology
어떤 Compound Proposition을 구성하는 p, q등 변수들의 값에 관계없이, 항상 참이 되는 명제
모순(Contradiction)
어떤 Compound Proposition을 구성하는 p, q등 변수들의 값에 관계없이, 항상 거짓인 명제
아래 표는 가장 간단하게 만든 tautology와 contradiction의 예시이다.
| $ p $ | $ \neg p $ | $ p \vee \neg p $ (Tautology) |
$ p \wedge \neg p $ (Contradiction) |
| T | F | T | F |
| F | T | T | F |
$ p \leftrightarrow q $ 가 tautology이면, p와 q는 동치(logically equivalent)라고 하고, $ p \equiv q $ 라고 표기한다.
역(Converse), 이(Inverse), 대우(Contrapositive / Transposition)
$ p \to q $ 일때,
역: $ q \to p $
이: $ \neg p \to \neg q$
대우: $ \neg q \to \neg p$
어떤 명제 $ p \to q $와 대우 $ \neg q \to \neg p$ 는 항상 동치이다.
아래 표는 기본적인 동치들이다.


만족가능(Satisfiable), 불능(Unsatisfiable)
명제를 참으로 만드는 변수들의 조합이 존재하면 만족가능(Satisfiable), 존재하지 않으면 불능(Unsatisfiable)이다.
'개인 공부' 카테고리의 다른 글
| [전산기조직] 논리 디자인의 기초 - Combinational Logic 편 (0) | 2025.03.02 |
|---|---|
| [정보보호개론] 보안의 속성(CIA triad, AAA triad) (0) | 2025.02.28 |
